JFE-TEC News
No.12「色を測る(3)」
JFE-TEC News No.12号 ダイオキシン類の迅速分析法 他 記事一覧

全文 PDF (462.5 KB)
No.12 ダイオキシン類の迅速分析法 他
色を測る(3)~XYZ表色系と色差の数値化~
XYZ表色系
前回お話ししたRGB表色系の問題点を改善するためにXYZ表色系が考案されました。3つの原刺激として別なX、Y、Zを選び、 1)等色関数が負にならない、 2)Yに明るさの情報を持たせるなど、表色や後の計算に都合の良い性質を持たせようというものです。数学の3次元の座標変換と同じ原理で一組の座標変換式が決定され、RGBからXYZへ変換されます。この結果、XYZ表色系の等色関数は図1となり、負の部分がなくなるなど改善されていることが分かります。XYZ表色系で、具体的なX、Y、Zの値と実際の色との関係がどうなっているかを知るためにパソコンで計算し、表現してみました。図2がその結果で、X+Y+Z=1で表される平面上に図示してあり、色度図と言われています。X、Y、Zの値が大きくなるとそれぞれ赤、緑、青の成分が大きくなることが分かります。このXYZ表色系は1931年に国際照明委員会(CIE)で標準の表色系として採択されています。
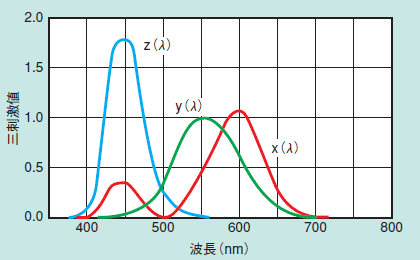
図1 XYZ表色系の等色関数
均等色空間(L*a*b*表色系)
さて、このように構築されたXYZ表色系は、図2で緑色の領域が大きいことからも分かるように、2つの色の差を見た場合、人が感じる差と色空間の距離の差が同じでない不都合があります。そこで人が感じる差と色空間の距離の差が比例するような、すなわち均等色空間を持った表色系が次に導出されました。その一つがL*、a*、b*表色系です。XYZ表色系から1組の関数変換式で変換できます。L*、a*、b*の値と実際の色との関係をパソコンで計算した結果を図3に図示しました。図2と比較して、均等色空間になっているのが分かります。色差ΔEはL*、a*、b*空間の2点の距離、
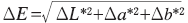
で表されます。
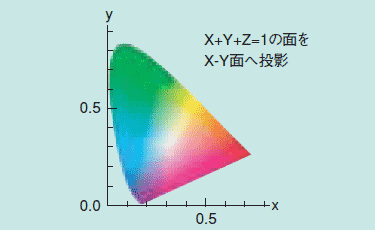
図2 XYZ表色系の色度図
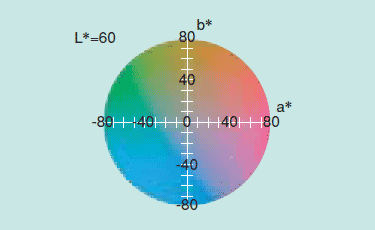
図3 L*a*b*表色系の色の表現例
L*が明るさ、a*、b*が色合いを表す。
図はL*=60のときのa*、b*による色の変化を示す。
このようにXYZ表色系を基本に、目的に応じて色々な表色系を導出できます。
関連リンク・関連記事
このページに関する
お問い合わせはこちらから
- JFEテクノリサーチ株式会社 営業総括部
- 0120-643-777


